Hydraulic Design of Sand Filters
for
Stormwater Quality

by
Ben R. Urbonas, P. E.
Chief, Master Planning Program

Introduction

This article is an abbreviated version of a full paper submitted for publication in a professional journal. It was modified to fit the Denver area's meteorology and the space available in this Flood Hazard News. The original paper is based on research efforts by the District, including filed data collection and analysis, of the hydraulic performance of sand filters under field conditions. Local data were combined with data from others in the U. S. to suggest pollutant removal by sand filters.

Design Hydrology and TSS Load

Because of the temporal variability of stormwater runoff, a media filter needs a detention volume upstream of it to equalize the runoff rates during a rainstorm. This detention volume has be drained out (i.e., fully evacuated) in a reasonable amount of time to provide room for the next runoff event. Urbonas and Ruzzo (1986) suggested a water quality capture volume (WQCV) equal to ½ inch of runoff from impervious surfaces in the tributary watershed. Subsequent studies of rainfall records in the United States and field performance of BMPs now suggest that this WQCV needs to be based on runoff somewhere between an average (i.e., mean) storm depth (Driscoll, et al., 1989) and the maximized depth (Guo and Urbonas, 1996). Equation 1 is now suggested (Urbonas, et al., 1996a) for making the first order estimate of WQCV.

                                                                            (1)

                    (2)

In which,

a = coefficient for the maximized or mean runoff volume from Figure 1

C = catchment's runoff coefficient found using Equation 2

P₆ = average runoff producing storm depth (0.43 inches in the Denver Area)

P_o = WQCV in inches

i_a = I_a/100

I_a = percent of the total area covered by impervious surfaces

Figure 1 - Values for coefficient  a   in Equation 1.

The average annual load of total suspended solids (TSS) in runoff can be estimated using:

(3)

In which,

L_a = average annual TSS load from the tributary catchment in pounds

A_c = area of tributary catchment in acres

P_A = average annual total stormwater runoff from the catchment in inches

n = average number of runoff producing storms per year (n = 30 in Denver)

E_s = average event mean concentration (EMC) of TSS in stormwater in mg/l

This annual load of TSS, along with the removal rates by the upstream detention/retention and by the filter determines the size of a media filter.

Filter Configurations

Figure 2 schematically illustrates three basic arrangements of upstream WQCV and the filter media. The upstream WQCV equalizes stormwater runoff rates to match the filter's flow-through capacity. When this capture volume is exceeded by a large storm, the excess runoff ponds on the surface upstream of the filter, or it bypasses the filter. In Case 1 the filter is preceded by an extended detention basin. In Case 2 the filter is preceded by a retention pond with a surcharge extended detention above the permanent pool. For both cases the detained volume is evacuated through an outlet designed to empty out the volume over a desired time period, namely its drain time. If the outlet is oversized, the drain time is governed by the flow-through rate of the filter itself. This is the design condition shown as Case 3, where at least a part of the detention volume is directly above the filter's surface.

Figure 2 - Three Arrangements of Filters with Detention

The detention/retention basin upstream of the filter removes some of the TSS in the runoff. We need to estimate how much TSS is removed this way to know how much TSS is left for removal by the filter. The intent of these estimates is to use reasonable, somewhat conservative rates that will result in a realistic filter size. Table 1 provides the suggested TSS removal rates for designing media filters.

Table 1. Suggested Removal Rates by Retention and Detention Upstream of a Media Filter

For Cases 1 and 2 defined in Figure 2 the concentration of TSS leaving the filter facility can be estimated using Equation 4.

                                                             (4)

In which,

E_sfr = the change in suspended solids concentration through the filter in mg/l

R_T = total system's average percent removal rate of TSS (95% recommended)

R_D = the percent removal rate for the retention or detention basin upstream of the filter bed from Table 1

For Case 3 the above analysis needs to be modified. The water column that is above the filter's surface receives no pretreatment and all the TSS in this water is subject to removal by the filter. Thus, for Case 3 reduction in the EMC of TSS by the filter installation can be expressed by

                                                        (5)

In which,

r_R = [A_R / (A_R+A_f)], ratio of the retention basin's surface area to the total system's surface area (When all detention storage is above the filter, r_R = 0 and all the TSS load is removed by the filter)

A_R = surface area of the retention pond's permanent pool in square feet

A_f = surface area of the filter bed in square feet

Filter’s Flow Through Rate

The classic relationship for water percolating through uniform soil media, such as sand, breaks down for a slow sand filter when fine sediment accumulates on top of its surface. Field observation and laboratory tests (Neufeld, 1996; Urbonas et al., 1996b) show that the flow-through rate for a sand filter (and other media as well) quickly becomes a function of the sediment being accumulated on the filter's surface. This relationship for a sand filter (i.e., Figure 3) appears to be not sensitive to the hydraulic surcharge on the filter's surface and can be expressed by Equation 6.

                                                                           (6)

In which,

k = empirical flow-through constant (see Figure 3)

c = empirical exponential decay constant (see Figure 3)

L_m = TSS load accumulated on the filter's surface in pounds per square foot

Figure 3:  Flow-through-rate of sand filter as a function of TSS removal.

TSS Load Removed By The Filter

Recognizing that not all runoff during any given year will pass through the filter installation, the average annual load removed by the filter facility can be expressed by Equation 7.

                (7)

 

In which,

L_afr = average annual TSS load removed by the filter in pounds

b = the fraction of all average annual runoff volumes that is treated by the filter facility (i.e., not bypassed)

The fraction of all runoff volume from the tributary area that will be treated through the filter facility is, in part, a function of the WQCV upstream of the filter. Depending on whether the basin is bypassed or overtopped will also determine the amount of treatment provided to the excess volumes during large storms. If the maximized capture volume is provided, approximately 80% to 90% of all runoff volume can be treated by the filter installation. If, however, the mean capture volume is used, approximately 65% to 70% of the total annual runoff volume will be fully processed through the filter.

The filter will also need to be maintained to stay in operation. The contaminated and clogged layers will need to be removed and replaced with new media and eventually (say after five to ten surface cleanings) the entire media filter will need to be replaced. Equation 8 can be used to estimate the TSS load removed by each square foot of the filter during each maintenance cycle.

                    (8)

 

In which,

L_m = average TSS load removed by each square foot of the filter during each maintenance cycle in pounds per square foot per maintenance cycle

m = number of times per year the filter is cleaned and reconditioned. Use a fraction (i.e., 0.5) if more than one year between cleanings

A_fm = surface area of the filter based on annual TSS load removed in square feet

Sizing The Filter

Equation 8 can be rearranged to estimate the filter's area based on TSS removed.

              (9)

Equation 10 can be used to estimate this area based on the desired drain time of WQCV.

(10)

 

In which,

Q = the design flow-through rate through the sand filter's surface in inches/hour

T_d = the time it takes volume P_o to drain out at rate q in hours

A_fh = surface area of the filter based on hydraulic sizing in square feet

The designer now has to find the filter area that comes close to satisfying both conditions and the following design procedure to accomplish this:

Design Procedure

1. Determine E_s, the average EMC of TSS for the tributary catchment. Use local TSS data when available. In absence of local data, use the closest regional averages reported in the Nationwide Urban Runoff Evaluation final report (EPA, 1983).
   
2. Calculate the average annual TSS load in stormwater runoff from the design catchment. Use Equation 2 and Equation 3 to estimate L_a.
   
3. Select filter-detention/retention configuration and preselect its desired drain time. Cases 1 and 2 are suggested for catchments with more than one acre of impervious surface, while Case 3 is suggested for smaller sites.
   
4. Estimate E_sfr, the reduction in the EMC of TSS provided by the filter itself. Based on Case 1, 2 or 3 with a value for r_R select a value from Table 1 for the removals by the detention or retention portion of the facility and use it in Equation 4 or 5.
   
5. Estimate the average annual TSS load removed by the filter. Use Equation 7 to calculate a value for L_afr (assume b = 0.90 if WQCV = P_o).
   
6. Determine the filter’s annual maintenance frequency. Typically one cleaning per year is suggested as a starting point.
   
7. With the aid of Figure 3 select the desired unit TSS load removed, L_m per each cleaning.
   
8. Set the WQCV for this installation. It is recommended that, as a minimum, a volume equal to the runoff between the mean storm and the maximized volume be used for design. Use equations 1 and 2.
   
9. Make first estimates of the filter’s area. Calculate the filter’s area, A_fm, using Equation 9 and Equation 10.
   
10. Compare the two filter areas calculated in Step 9. If the two calculations differ by more than 20%; average the two areas; calculate a new value for the unit load removed by the filter, L_m; find a new q using Equation 7 and repeat Step 9. Otherwise use the larger surface area of the two.

Design Examples

Example 1. At a commercial site in Denver the media filter will be preceded by an upstream extended detention basin. The known site conditions are:Example 1. At a commercial site in Denver the media filter will be preceded by an upstream extended detention basin. The known site conditions are:

Step 1:

Tributary Area, A_c = 1.5 acres

Expected EMC of TSS, E_s = 225 mg/l

Average storm depth, P₆ = 0.43 inches

Average number of runoff storms per year, n = 30

Catchment's total imperviousness,  I_a = 85%

Step 2: Using Equation 2 find its runoff coefficient:

C = 0.66

Using Equation 3 calculate the annual TSS load from the catchment:

L_a = 651 lbs

Step 3: Since the filter will be preceded by an upstream extended detention basin, we have Case 1 configuration. The WQCV will drain in 12 hours.

Step 4: Using T_d = 12 hours, Table 1 suggests R_D = 50%. Assuming 95% overall removal rate for the detention-filter system, estimate using Equation 4 the reduction in TSS produced by the filter itself.

E_sfr = 101 mg/l

Step 5: Using Equation 7 estimate the average annual TSS load removal by the filter.

L_afr = 263 lbs

Step 6: Determine the filter's annual maintenance frequency. Assume m = 1 (i.e., once per year).

Step 7: To keep the size of the filter small while not imposing a very frequent maintenance schedule we choose to design the filter to drain at approximately 2.0 inches per hour. This means L_m = 0.32 pound/square foot in Figure 3.

Step 8: Using T_d = 12 hours and C = 0.66 from Step 2 and a from Figure 1 in Equation 1, find the maximized WQCV:

P_o = 0.32 watershed inches = (1720 ft³)

Step 9: Using Equations 9 and 10:

A_fm = 822 ft²

A_fh = 871 ft²

Step 10: The two areas are within 20% of each other. Choose the larger of the two.

A_f = 870 sq. ft. (after rounding off)

 

Example 2Example 2. Same as Example 1 except use a filter inlet, namely Case 3, with r_R = 0.5.

Steps 1 through 3 are the same as in Example 1.

Step 4: Using Equation 5 for a "retention basin" with a 12-hour drain time find:

E_sfr = 124 mg/l

Step 5: Using Equation 7 we find

L_afr = 322 lbs

Step 6: Assume m = 1.

Step 7: Using the same reasons stated in Example 1 we find: L_m=0.32 lbs/ sq. ft.

Step 8: Same as in Example 1 @ T_d = 12 hrs.: P_o=0.32 inches (1,720 cu. ft.)

Step 9: Using Equations 9 and 10:

A_fm = 1006 ft²

A_fh = 871 ft²

Step 10: The two are within 20% of each other. Use the larger of the two.

A_f  = 1,000 ft² (after rounding off)

Expected Water Quality Performance

Figure 4 illustrates two cases during larger storms, namely overflow of the excess and the bypass of the excess. To make a valid assessment of the average annual EMC for any constituent reaching receiving waters, to flow-weight the concentrations of the effluent and the excess runoff from all the storms that occur, on the average, any given year. For Case 1 shown in Figure 4 this is given by Equation 11.

Figure 4 - Stormwater Runofff Connection Arrangements for a Filter System.

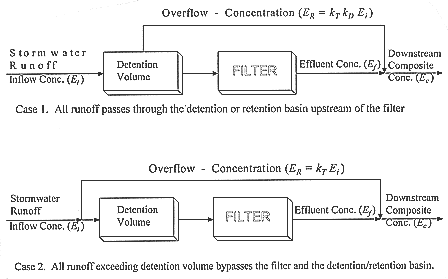
                           (11)

and for Case 2 by Equation 12

                                      (12)

In which,

E_c = average annual EMC downstream of the filter facility, in mg/l

E_i = average annual EMC in the runoff inflow to the WQCV, in mg/l

E_f = average annual concentration in the filter's effluent, in mg/l

r_pf = fraction of the average annual runoff volume that flows through the filter

k_B = fraction of the original EMC in the runoff that remains in the water after overflows

k_T = coefficient of the EMC that represent the post "first-flush" fraction of the average EMC in stormwater runoff

If the maximized coefficients in Figure 1 are used, one can expect r_p  = 0.8 to 0.9. If, however, the runoff from the mean storm is used, one can expect r_pf = 0.65 to 0.7.

Currently it is not possible to suggest definitive values for k_D and k_T, which coefficients depend on the constituent being considered and the actual design. However, a literature review by the author suggests the following tentative ranges for TSS:

k_D = 0.3 to 0.5 k_T  = 0.7 to 0.9

Table 2 summarizes, after screening out the outliers, the findings of filter tests at four cities in the United States, namely, Alexandria, VA; Austin, TX; Anchorage, AK; and Lakewood, CO. Data for the first three were consolidated by Bell et al. (1996) and the data for the Lakewood site were obtained by the Urban Drainage and Flood Control District in 1995. Note the high variability in the influent concentrations for all constituents and that the ratios between the high and the low concentrations are significantly less for the effluent. The variability in the influent quality accounts for most of the range in the reported removal percentages.

Table 2. Field Measured Performance Ranges of Sand Filters

In Example 1 an extended detention basin was used upstream of the filter. It is relatively easy to design this arrangement so that all runoff will pass through the detention basin and the excess runoff will overtop the pond. Let's further assume that k_D = 0.35 and k_T = 0.75 and as a first order estimate assume that 80% of the average annual runoff volume will pass through the basin and the filter. Using an average effluent TSS concentration of 16 mg/l (Table 2), the average annual EMC of TSS downstream of the filter installation is:

E_c = 25 mg/l

Comparing this to the average EMC for TSS in stormwater runoff at that site (i.e., 225 mg/l), this installation will have 82% average annual removal efficiency for TSS.

Acknowledgments

The author wishes to acknowledge the support of the Urban Drainage and Flood Control District and City of Lakewood in the building and testing of this test filter installation. Many thanks to L. Scott Tucker, the District’s Executive Director, for his continuing support of scientific exploration.

The author is also grateful to John Doerfer, Richard Ommert, Curtis Neufeld, Jerry Goldman, Chris Jacobson, Warren Bell, Richard Horner, Betty Rushton, Eugene D. Driscoll, Jonathan E. Jones, Jiri Marsalek, Bill Pisano, William P. Ruzzo, George Chang and James C.Y. Guo for their help, support and/or review and comments on the original paper and to Galene Bushor for sorting through and making sense of the author's hand-written manuscripts.

References

Bell, W., Stokes, L., Gavan, L.J. and Nguyen, T. 1996 (undated). Assessment of the Pollutant Removal Efficiencies of Delaware Sand Filter BMPs. City of Alexandria, Department of Transportation and Environmental Services, Alexandria, VA.

Driscoll, E.D., Palhegyi, G.E., Strecker, E.W. and Shelley, P.E. 1989. Analysis of Storm Events Characteristics for Selected Rainfall Gauges Throughout the United States. U.S. Environmental Protection Agency, Washington, D.C.

EPA. 1983. Results of the Nationwide Urban Runoff Program, Final Report. U.S. Environmental Protection Agency, NTIS PB84-18552, Washington D.C.

Guo, J.C.Y. and Urbonas, B. 1996. "Maximized Detention Volume Determined by Runoff Capture Ratio," J. Water Resources Planning and Management. Jan/Feb, p. 33-39, American Society of Civil Engineers, Reston, VA.

Neufeld, C.Y. 1996. "An Investigation of Different Media for Filtration of Stormwater." Masters Thesis, Department of Civil Engineering, University of Colorado at Denver, Denver, Colorado.

Urbonas, B. R., and Ruzzo, W. 1986. "Standardization of Detention Pond Design for Phosphorus Removal," Urban Runoff Pollution. NATO ASI Series Vol. G10, Springer-Verlag, Berlin.

Urbonas, B., Roesner, L.A., and Guo, C.Y., L.S. 1996a. "Hydrology for Optimal Sizing of Urban Runoff Treatment Control Systems," Water Quality International. International Association for Water Quality, London, England.

Urbonas, B.R., Doerfer, J.T. and Tucker, L.S. 1996b. "Stormwater Sand Filtration: A Solution or a Problem?" APWA Reporter. American Public Works Association, Washington, DC.